Tots els Sistemes d’Informació Geogràfica (SIG) tenen el concepte de Zona d’Influència, normalment anomenat ‘buffer’, que consisteix en agafar una classe d’entitat (taula d’entitats) i generar en el seu entorn una àrea que amplia la frontera de les entitats una certa distància i respon a la idea de zona d’influència o zona de proximitat o de veïnatge.
Per tant si la classe d’entitat de la que volem definir el ‘buffer’ és una àrea, tal com hem dit, el seu ‘buffer’ és una altra àrea que comprèn l’entitat i té més o menys la mateixa forma, però si la classe d’entitat és lineal el seu ‘buffer’ és una àrea de tipus rectangular que pot estar arrodonida en els extrems i si la classe d’entitat és puntual el seu ‘buffer’ és una àrea de tipus circular.
Un paràmetre característic de les zones d’influència és el ‘radi’ o distància, en realitat el concepte més adequat és el de distància ja que ens indica a quina distància de l’entitat base es troba el límit de la seva zona d’influència, però que en el cas d’entitats puntuals, com que la zona d’influència és circular, sí que coincideix amb el radi d’aquest cercle.
- Fig 1: Zones d’Influència sobre les Zones Verdes a una distància de 50 m.
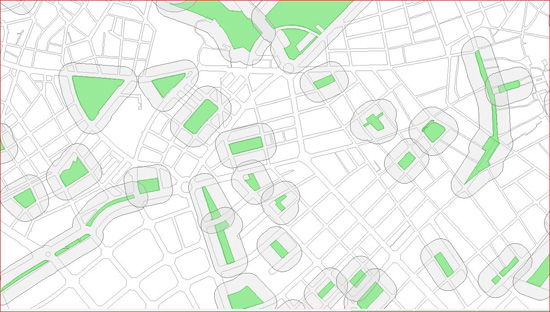
A la figura 1 podem veure un exemple de les zones d’influència sobre entitats tipus àrea, com és el cas de les zones verdes accessibles de la ciutat de Mataró, en aquest cas s’ha considerat una distància fixa de 50 metres. Això podria tenir un sentit de comptar , per exemple, quants ciutadans viuen a menys de 50 metres d’una zona verda.
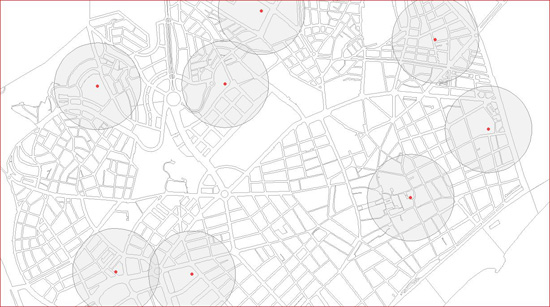
Un altre cas molt comú d’utilització de les zones d’influència seria veure quants ciutadans estan a més d’una determinada distància d’un centre proveïdor de serveis, com un Centre d’Assistència Primària (CAP) o un centre docent o un centre cívic, en aquest cas són molt útils els ‘buffers’ a l’entorn d’aquestes entitats, que normalment són representades com a entitats puntuals i per tant les seves zones d’influència seran circulars. Això ho podem veure a la figura 2 pel cas d’Escoles Bressol Municipals de la ciutat de Mataró.
- Fig 2: Zones d’Influència a l’entorn de Escoles Bressol Municipals a 250 m
En aquesta figura es veuen els típics cercles que corresponen a les zones d’influència de les entitats puntuals i que podrien servir, tal com hem dit, per veure quanta població està a menys de 250 metres d’una Escola Bressol Municipal i quanta a més, per exemple.
Aquesta característica de dibuixar ‘buffers’ a l’entorn d’entitats és molt utilitzada en SIG quan es volen fer operacions espacials, com ara unió, intersecció, combinacions analítiques, agregacions etc. En el cas de les Escoles Bressol, es pot fer una agregació de tota la població (o dels infants entre 0 i 2 anys) que hi ha dins de cada zona d’influència a partir de les dades que tenim prèviament agrupades per Illes de cases, parcel·les o portals, tal com s’ha descrit en un altre ‘post’ en aquest mateix bloc, indicant que es sumen tots els habitants que pertanyen a les entitats (siguin aquestes Illes, parcel·les o portals) que estan contingudes dins de la zona d’influència corresponent.
De totes maneres, en totes les operacions que tenen a veure amb la població i amb els seus desplaçaments per la ciutat, aquesta mesura de la proximitat directe que ens proporciona el ‘buffer’ dels SIG no sempre ens és útil, ja que si volem dir ‘nens que hi ha a menys de 250 m de l’Escola Bressol’ aquest concepte de ‘buffer’ ens mostra els nens que viuen a menys de 250 m, però en línia recta, ja que és el radi de la zona d’influència. El que seria més real seria indicar els nens que hi ha a 250 m seguint la xarxa de carrers, comptant que els nens aniran a l’escola circulant pel carrer. També seria útil considerar en comptes de distància, el seu equivalent en temps, nens que hi ha a menys de 5 minuts del centre, i en aquest cas tenint en compte les facilitats o inconvenients que presenten els carrers, pendents, obstacles ,escales etc.
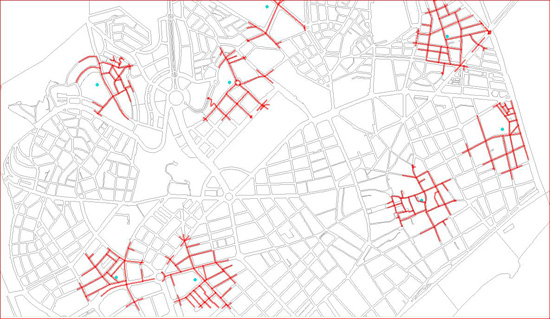
Això ens ha de portar a definir una nova zona d’influència lligada a la xarxa de trams de carrer (anomenem tram el segment de carrer entre cruïlla i cruïlla). En primer lloc considerarem la xarxa com a una entitat lineal arborescent que creix a partir de l’entitat puntual origen (en aquest cas serien les Escoles Bressol). Vegeu la figura 3
- Fig 3. Graf de Trams de Carrer a partir de les Escoles Bressol fins a 250 m de distància
Efectivament a la figura es poden veure els recorreguts a partir de l’entitat origen que faria un vianant anant en qualsevol direcció (sense passar dues vegades pel mateix lloc) i recorrent un màxim de 250 metres. Com es pot veure els possibles recorreguts depenen de la morfologia de la xarxa de carrers en cada lloc de la ciutat, a part de la pròpia distància a recòrrer. En aquest cas el sentit de distància és molt més real que considerant les zones d’influència clàssiques amb distància a vista d’ocell.
Com que volem tenir una zona d’influència amb les mateixes característiques que la definida de forma clàssica, hem de convertir aquest conjunt de trams en un àrea, agafant precisament un ‘buffer’ sobre aquesta entitat lineal (abans hem hagut de convertir el conjunt de trams en una entitat lineal única)
- Fig 4. Zones d’Influència sobre el Graf de Trams de Carrer, distància 250 m
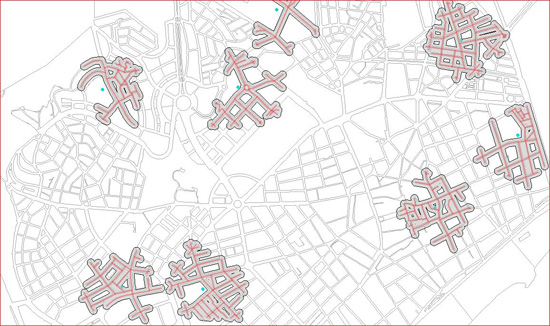
A la figura 4 es pot veure l’efecte d’agafar un ‘buffer’ sobre cada conjunt de trams desplegats a 250 m de la seva entitat origen. Aquest ‘buffer’ s’agafa a 20 m de les línies del graf de trams.
D’aquesta manera es poden continuar aplicant les operacions espacials que ens calguin pels nostres càlculs com si fossin àrees circulars, però amb l’avantatge d’uns resultats molt més realistes quan treballem amb població i distàncies.
